Volver a Guía
Ir al curso
CURSO RELACIONADO
Física 03
2026
TORTI
¿Te está ayudando la guía resuelta?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰
Ir al curso
FÍSICA 03 UBA XXI
CÁTEDRA TORTI
3.
Una mujer en el aeropuerto mueve su maleta de $20,0 \mathrm{~kg}$ a una velocidad constante tirando de la correa con una fuerza de $35,0 \mathrm{~N}$ con una dirección $\theta$ determinada como muestra la figura, la fuerza de fricción entre la maleta y el piso es de 20 N.

a) ¿Qué ángulo forma la correa con respecto a la horizontal cuando la mujer jala de ella?

a) ¿Qué ángulo forma la correa con respecto a la horizontal cuando la mujer jala de ella?
Respuesta
Vamos a arrancar armando el diagrama de cuerpo libre de la maleta...
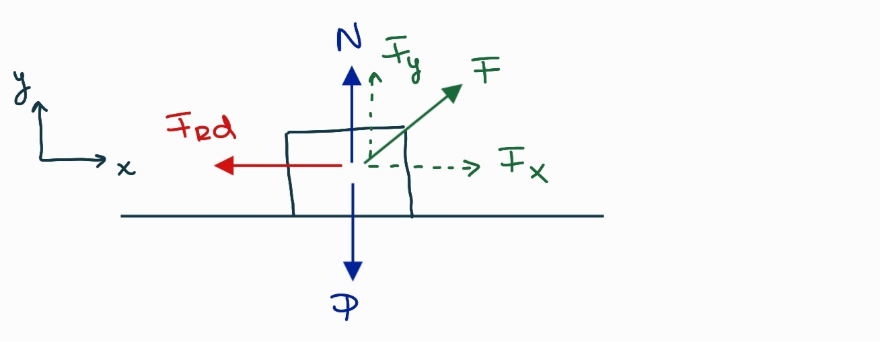
Reportar problema

El peso de la maleta es
$P = m \cdot g = 20.0 \text{ kg} \cdot 9.8 \, \frac{m}{s^2} = 196 \text{ N}$
Y la fuerza $F$ nos quedaría descompuesta así:
$F_x = 35 \text{ N} \cdot \cos(\theta)$
$F_y = 35 \text{ N} \cdot \sin(\theta)$
Además, del enunciado sabemos que
$F_{\text{roz}} = 20 \text{ N}$
Ahora, muchísima atención acá -> Nos dicen que la maleta se está moviendo con velocidad constante... es decir, ¿cuánto vale la aceleración en el eje $x$? Claaaaro, vale cero! La maleta no está acelerando si su velocidad es constante! Entonces, cuando planteo segunda ley en el eje $x$ me queda así...
$\sum F_x = m \cdot a_x$
$F_x - F_{\text{roz}} = 0$
$35 \text{ N} \cdot \cos(\theta) - 20 \text{ N} = 0$
Y ahora terminamos de despejar $\theta$
$\theta = 55.2°$
🤖
¿Tenés dudas? Pregúntale a ExaBoti
Asistente de IA para resolver tus preguntas al instante🤖
¡Hola! Soy ExaBoti
Para chatear conmigo sobre este ejercicio necesitas iniciar sesión
ExaComunidad
Conecta con otros estudiantes y profesoresNo hay comentarios aún
¡Sé el primero en comentar!
